While modern convolutional neural networks achieve outstanding accuracy on many image classification tasks, they are, compared to humans, much more sensitive to image degradation. Here, we describe a variant of Batch Normalization, LocalNorm, that regularizes the normalization layer in the spirit of Dropout while dynamically adapting to the local image intensity and contrast at test-time. We show that the resulting deep neural networks are much more resistant to noise-induced image degradation, improving accuracy by up to three times, while achieving the same or slightly better accuracy on non-degraded classical benchmarks. In computational terms, LocalNorm adds negligible training cost and little or no cost at inference time, and can be applied to many already-trained networks in a straightforward manner.
Deep neural networks tend to fail dramatically when noisy versions of images are presented.
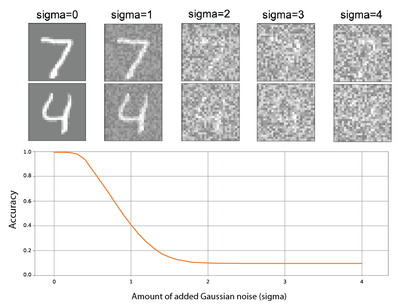
Intuitively, one possible reason for this behavior is the normalization layer that is applied in almost all modern neural networks to make training feasible for (very) deep networks.
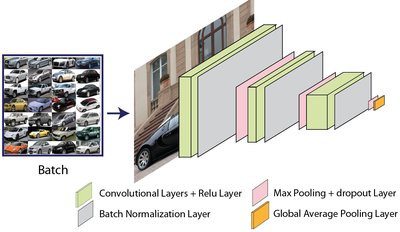
The best-known normalization method, Batch Normalization, computes the outputs of neurons in a single feature layer for a whole batch of images to obtain summary statistics (usually: mean and standard deviation). These statistics are then scaled by two trainable parameters, beta and gamma. This keeps the neural activities in useful ranges, which proved to be essential for the deep networks since developed. An example of such a network is shown below.
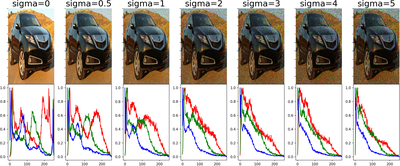
The fly in the proverbial ointment is that in the standard implementation of Batch Normalization, these summary statistics are computed over the training set and then fixed when evaluating performance on the test-set. Now what happens when images are distorted by noise? This is in fact well known: the summary statistics change. In the image below, a specific kind of noise is added (Additive Gaussian Noise), and below the images the histograms for the different colors (RGB) are plotted. The shift is easy to see.
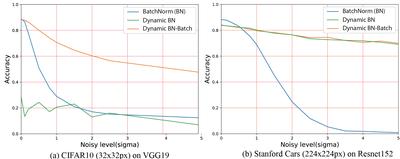
So why does Batch Normalization fix the summary statistics for testing? Two reasons: first, for small images, like the 32x32pixel sized Cifar10 images, summary statistics for a feature are only useful when computed over a set of images (a batch). Large images however, like the cars in the Stanford Cars dataset, the summary statistics from a single image are a lot more robust - note that if we take a set of test-images (a Batch) to compute summary statistics on at test-time, we get much better results on the small images. Secondly, both cases, the accuracy on the noise-less data suffers.
We solve this using a method we call LocalNorm. For local norm, we split, when training, the batch into groups, and maintain separate normalization parameters (beta,gamma) for each group. This effectively creates as many networks as there are groups, sharing all weights but not normalization scaling parameters.
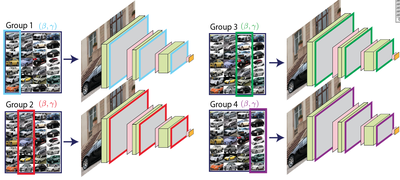
This effectively regularizes the Batch Normalization layer and makes the network robust to changes in summary statistics, also for different kinds of noise. Examples of images degraded with different types of noise are shown below, the graphs compares the accuracy for BatchNorm vs our LocalNorm for increasing amounts of noise.
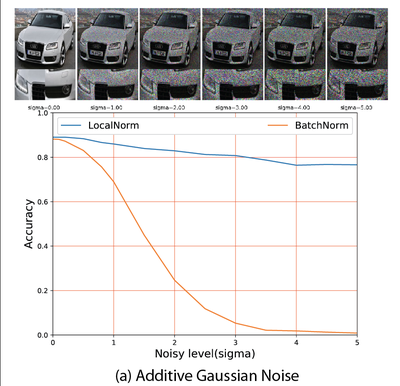
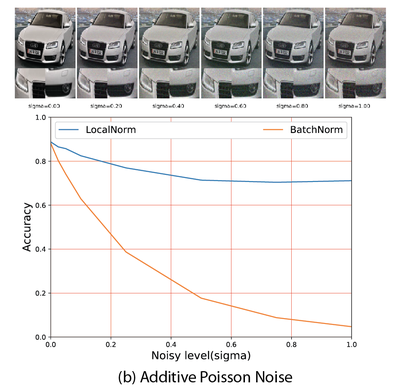
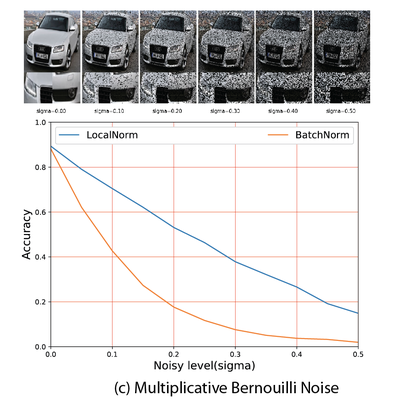
For large enough images, LocalNorm gives us the best of both worlds: robust and accurate networks that can be evaluated using single images at test time. For poorly lit or camouflage cars sampled from the web, even the brand and year is correctly recognized with LocalNorm:

Thus, with LocalNorm, we obtain deep neural networks that are much more resistant to noise-induced image degradation, improving accuracy by up to three times, while achieving the same or slightly better accuracy on non-degraded classical benchmarks. In computational terms, LocalNorm adds negligible training cost and little or no cost at test-time, and can be applied to many already-trained networks in a straightforward manner.
The full Arxiv paper with all the details is here; example implementation code is here (Github).
