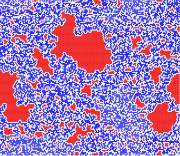
The percolation model can be illustrated through the following example. A porous rock consists of many holes. Some of these holes are connected by tiny channels in some random way. How many channels are needed so that it is likely that water can pass through the rock? The percolation model is a widely studied model of statistical physics. It shows that fine small-scale changes can manifest on large scale.
Kiss has studied various aspects of the percolation model. He improved some concentration inequalities to help the study of the model. These inequalities, for instance, give a better understanding of the voting power of the individuals at an election. He also investigated an extension of the percolation model where the speed of the propagation of the liquid is taken into account. He found upper bounds of the variance of this speed. Finally, Kiss studied an adaptation of the percolation model for polymerization. In this model small molecules merge, but large molecules do not interact with the other particles, causing large molecules to stop growing. He showed that in the two dimensional case, large molecules appear almost at the same time.
Kiss also investigated the so-called mean field case of the percolation model. In this set-up, the model turns into a critical state without any tuning when time evolves. Similar dynamics are believed to be responsible for avalanches, earthquakes and even fluctuations of financial markets. Better understanding of these dynamics can lead to a better understanding of these phenomena.
The project is funded by the Netherlands Organization for Scientific Research (NWO) as an investment in talent and curiosity-driven research.
More information:
Thesis: 'Topics in percolation theory'
By: Demeter Kiss (CWI Stochastics group)
Supervisor: Prof J. van den Berg (CWI/ VU University Amsterdam)
Date: Wednesday 3 July 2013, 13.45h
Location: Aula, De Boelelaan 1105, Amsterdam
Image: Percolation configuration with frozen clusters. Demeter Kiss, CWI
