MSc project: Exploring the Design Space of Optical Neural Networks for Intelligent Imaging Systems

Project description

This project builds on an ongoing collaboration between groups working on computational imaging and experimental photonics, where fiber-based imaging systems are explored using compressed sensing and randomized illumination. While the current work focuses on designing algorithms for compressed optical measurements, this proposal complements jointly designing the optics and the algorithm in a data-driven fashion. This opens possibilities for real-time, compact imaging systems. A schematic depiction is shown in Figure 1.

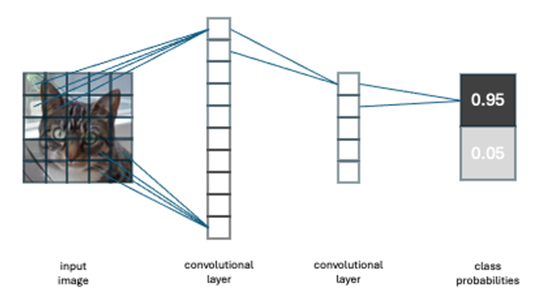
Figure 1 Schematic depiction of a convolutional neural network classifying an image of a cat.

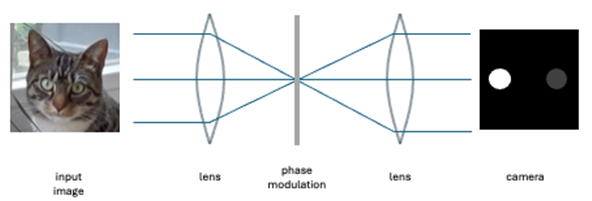
Figure 2: Schematic depiction of an optical neural network classifying an image of a cat

The scientific challenges are:

1. We need to mathematically characterize the expressive power and robustness of feasible ONN designs. Unlike conventional deep neural networks, many ONNs — particularly those implemented as passive, layered optical systems — lack nonlinear activations between layers. This makes their theoretical behavior quite distinct. We aim to explore this linear regime using tools from inverse problems, and random matrix analysis, where neural networks with fixed internal weights and only trained outputs have shown surprising expressive capabilities. Understanding these mathematical properties could clarify the limitations of passive ONNs and help guide the design of more effective task-specific architectures.
2. We need to computationally design an ONN for a specific task, which requires effective parametrization of the design space, and methods for training it on given data. What sets this task apart from regular machine learning, is that the ONN will need to be manufactured, potentially introducing small imperfections that make its performance deviate from the computational design. To this end, we will focus on developing algorithms for robust training to ensure that the design ONN will retain its performance even under small perturbations of the design.
3. We need to experimentally demonstrate ONN performance. We will integrate the designed ONN in an existing optical setup, which can be further modified following the computational design. Experimental feedback will be used to refine computational models, closing the loop between theory, computational design and experiment.

The mathematical and computational aspects will be carried out in close coordination with researchers specializing in inverse problems and learned sensing. Their experience includes high-dimensional optimization, differentiable optical simulation, and neural network training under physical constraints. The experimental aspect sill be carried out in close coordination with the contract manufacturer, to fine-tune the printing process for the envisioned application. To validate the designed ONNs, we will integrate the designed ONN in an existing optical setup. While the specific approach will be chosen collaboratively during the project, the group’s background ensures both methodological feasibility and flexibility.

Supervision & focus areas

Supervisors: Tristan van Leeuwen (CWI) and Lyuba Amitonova (Nanoscale Imaging and Metrology group at ARCNL):

Keywords: Imaging, Optics, Neural Networks, Optical Neural Network.

Further reading

1. Lin X, Rivenson Y, Yardimci N T, Veli M, Luo Y, Jarrahi M, Ozcan A. All-optical machine learning using diffractive deep neural networks. Science. 2018;361(6406):1004–1008.
2. Perfilieva, Irina, et al. "A critical analysis of the theoretical framework of the Extreme Learning Machine." Neurocomputing 621 (2025): 129298.