Moore's Law last April turned 50 years old.
Or less prosaically: Moore's Law became 33⅓ iterations of itself old.
When you turn a tap on,
you are adding a certain amount of water per minute to the
bath.
So if we look at the graph of the bath filling, we get something like this:
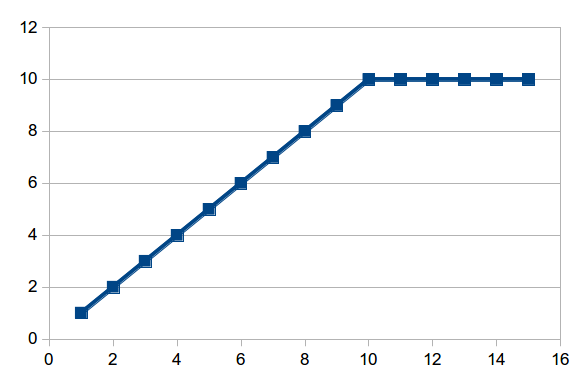
We call this a linear function.
However, for instance, when a bank gives you interest on a bank account, it is not adding a fixed amount every year, but an amount based on how much you already have in the bank.
For instance, if they offer a 3% interest, then every year your money gets multiplied by 1.03.
If you have €1000 in your account, then at the end of the year you will have €1000 × 1.03, which is €1030. At the end of the second, you will have €1030 × 1.03, which is €1060.90.
This is called an exponential function.
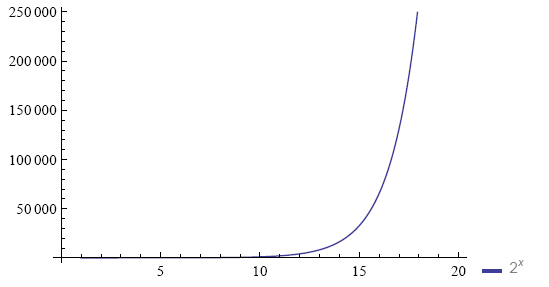
Note the 'knee' around iteration 15. People often talk about an exponential function 'passing the knee'. This is a mistake.
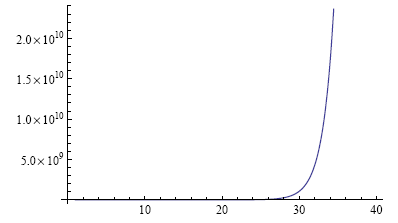
Note how there now seems to be nearly no action before iteration 26. The 'knee' is a fiction, a visual effect of the scaling used.
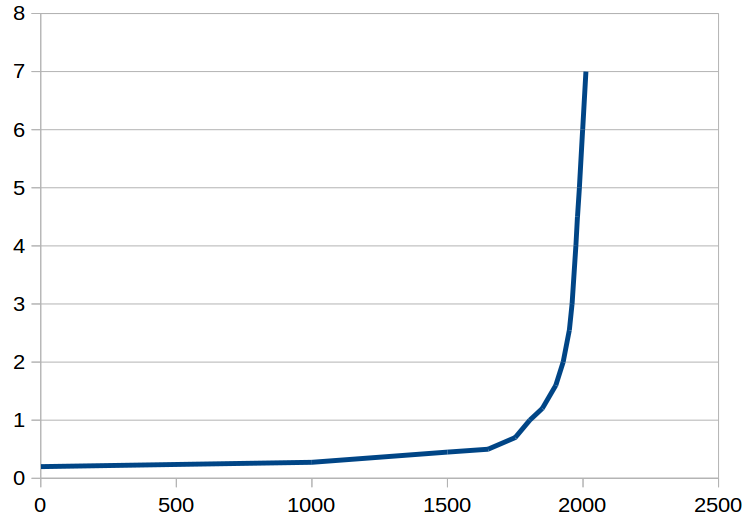
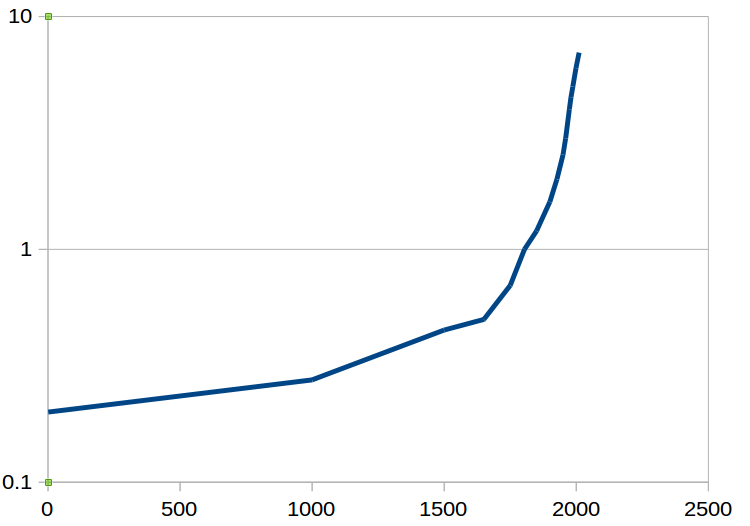
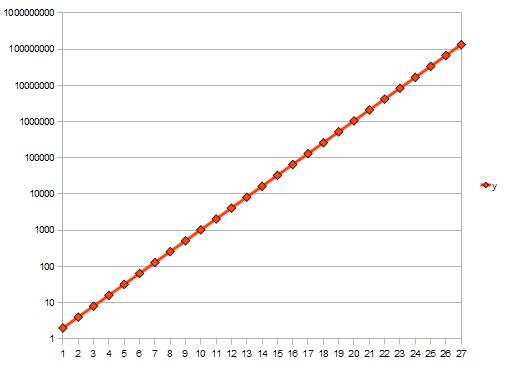It is better to graph exponential functions in a different way.
On the vertical axis, rather than going in steps of 1, 2, 3, ... we use steps of 1, 10, 100, 1000, ... Then the exponential graph looks like this:
(It actually doesn't matter what the step size is, as long as it is a multiplication: the graph still ends up looking the same).
Moore's Law is also a multiplication: a doubling every 18 months (which is
59% annual interest, if you are interested, or about 4% per month).
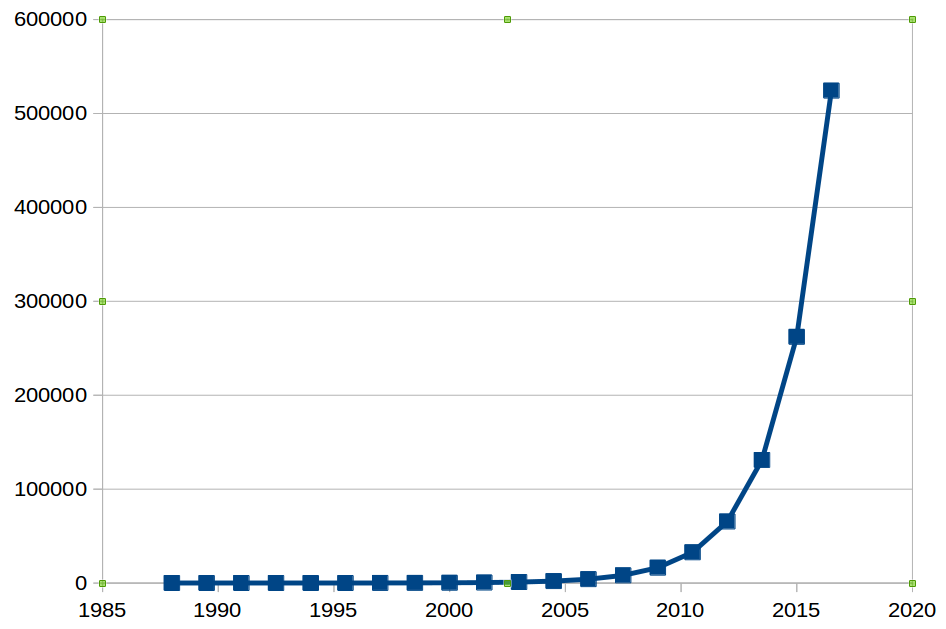
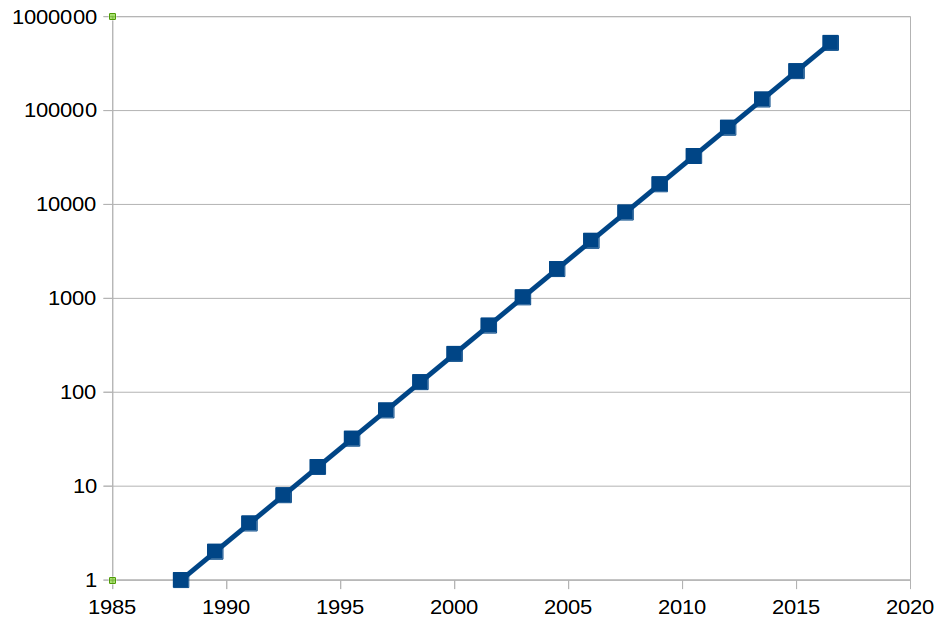
If we draw an idealised graph of Moore's Law since 1988, it looks something like this:
In other words, a computer now is approaching 500 000 times more powerful than in 1988.
Or put another way, each day you are getting 6500 computers from 1988 extra.
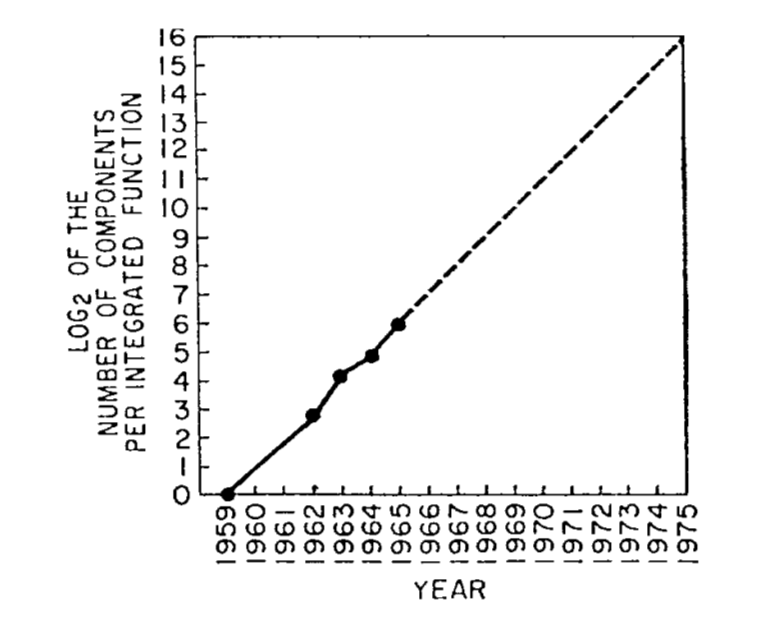
So this is what Moore's 1965 graph was saying. Components on integrated
circuits were doubling per year at constant cost (in 1975 he reduced that to 18
months per doubling).
Of course, computers don't get exactly
twice as powerful in exactly 18 months.
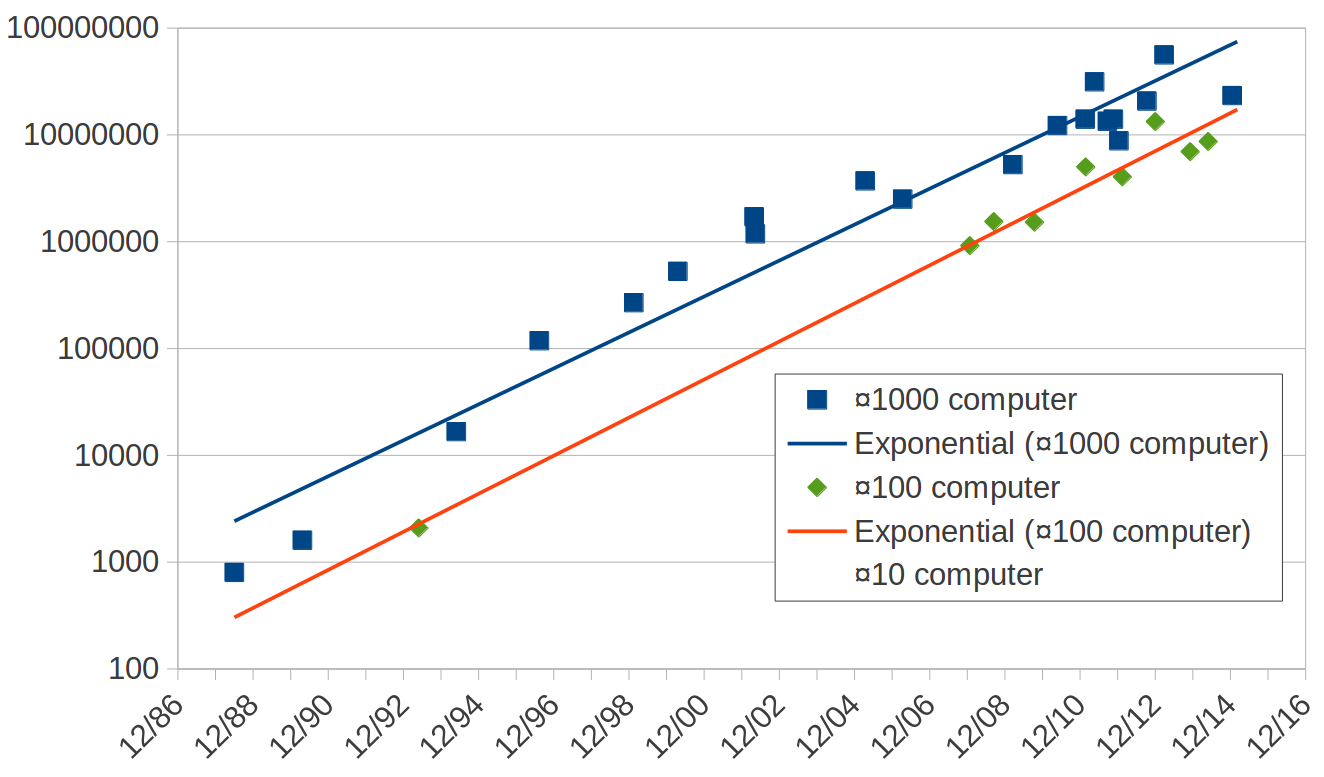
But I have been collecting data on the power of my computers since 1988.
In 1988 my laptop had a power of 800. My present one has a power of more than 25M. That is 15 doublings!
Often people don't understand the true effects of exponential growth.
A BBC reporter recently: "Your current PC is more powerful than the computer they had on board the first flight to the moon". Right, but oh so wrong (Closer to the truth: your current computer is several times more powerful than all the computers they used to land a man on the moon put together.)
Take a piece of paper, divide it in two, and write this year's date in one half:
Now divide the other half in two vertically, and write the date 18 months ago in one half:
Now divide the remaining space in half, and write the date 18 months earlier (or in other words 3 years ago) in one half:
Repeat until your pen is thicker than the space you have to divide in two:
This demonstrates that your current computer is more powerful than all other computers you have had put together.
Since current computers have a working life of about 5 years, this means that society as a whole at this moment has around 95% of the computer power it has ever had! (And this will always be true as long as Moore's Law is going).
The first time I head that Moore's Law was nearly at an end was in 1977. From no less than Grace Hopper, at Manchester University.
Since then I have heard many times that it was close to its end, or even has already ended. There was a burst of such claims last year, which caused a wag to tweet
"The number of press articles speculating the end of Moore's Law doubles every eighteen months."
As an
excellent example, in February last year, almost exactly three years after the
announcement of the first version, version 2 of the Raspberry Pi computer was
announced.
Since three years is exactly two cycles of Moore's Law, does the new Raspberry Pi deliver a four-fold improvement?
| And now we have a $5 version | 1/5th of the original price. |
| 1GHz ARM11 core | 40% faster than Raspbery Pi 1 |
| 512MB of RAM | 2 × Raspberry Pi 1 |
| Size 65mm x 30mm | vs 85.60 mm × 56.5 mm = 40% of the size |
In fact it doesn't even show signs of slowing down.
How does it compare with other exponentials?
Although computers are our most obvious example of exponential growth, there are many others.
.svg.png)
This shows a doubling period of about 12 years. It also shows the advantage of the log scale: the great crash of 1930 becomes visible.
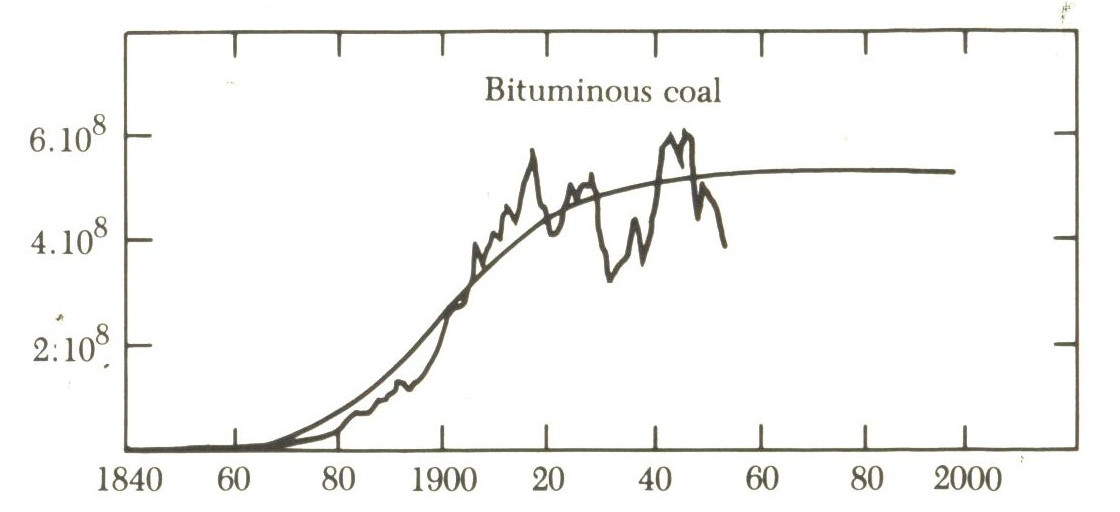
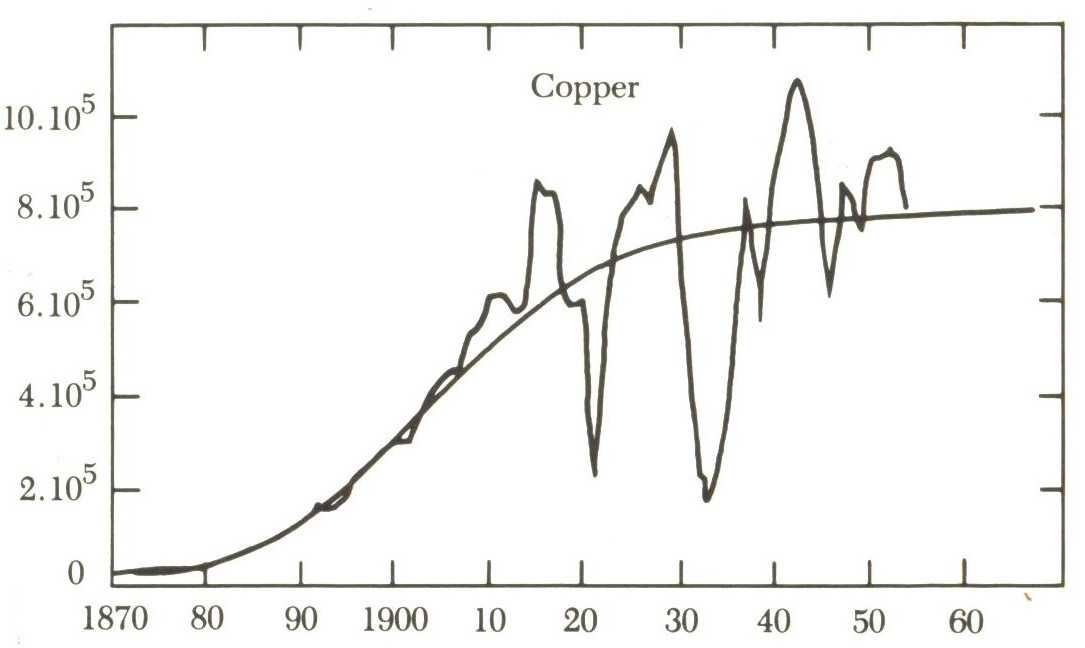
(These are all taken from a 1960's book "Big Science, little science...and beyond, by Derek J. La Solla Price . Most of them I haven't checked against modern data)
Entries in dictionaries of national biography
Labor force
Population (I checked this one, and got 58 years)
Number of universities
Gross National Product (I got 10 years for UK 1955-2012)
Important discoveries
Important physicists
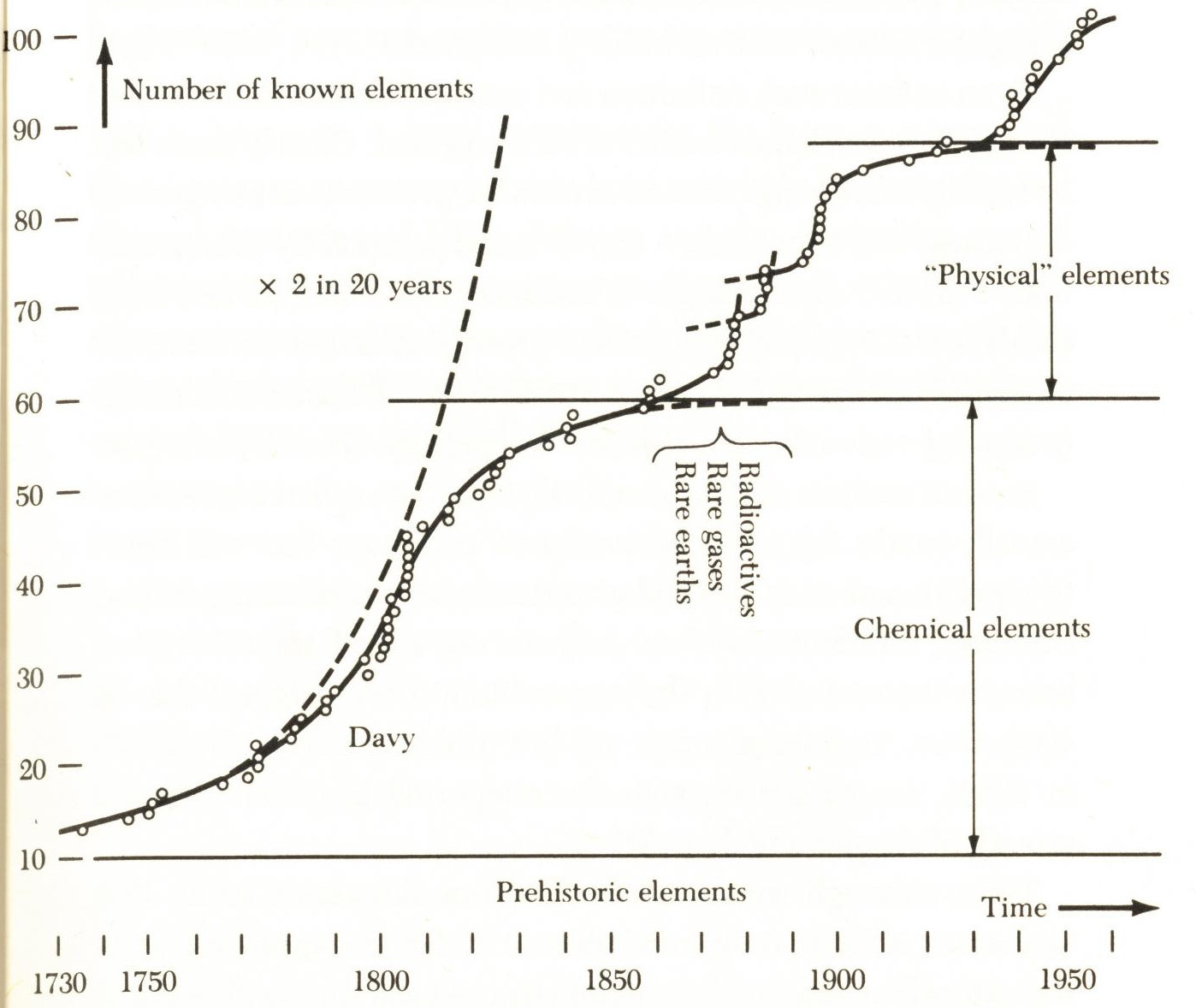
Number of chemical elements known
Accuracy of instruments
College entrants/1000 population
B.A., B.SC.
Scientific journals
Membership of scientific institutes
Number of chemical compounds known
Number of scientific abstracts, all fields
Number of asteroids known
Literature in many scientific disiplines
Number of telephones in United States
Number of engineers in United States
Speed of transportation
Kilowatt-hours of electricity
Number of overseas telephone calls
Magnetic permeability of iron
Million electron volts of accelerators. (I checked the original data, and I got about 1.7 years. Redoing it with modern data, I get more or less exactly 2 years.)
Components on an integrated circuit
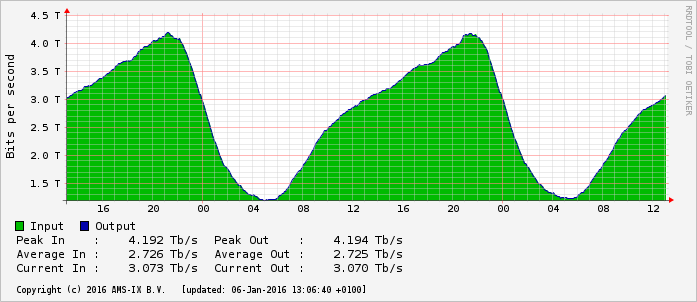
Internet Bandwidth
Amount of data produced worldwide
Amsterdam was 64KB/s in 1988, and now 4.3TB/s = 1.95 yearly growth over 27 years.
4.3TB/s... what does that mean.
Can we get a feel for what such a number means?
1 byte = 1 second
1 byte = 1 second
1KB = 17 mins
1 byte = 1 second
1KB = 17 mins
1MB = 12 days
1 byte = 1 second
1KB = 17 mins
1MB = 12 days
1GB = 34 years
1 byte = 1 second
1KB = 17 mins
1MB = 12 days
1GB = 34 years
1TB= 35 millenia
1 byte = 1 second
1KB = 17 mins
1MB = 12 days
1GB = 34 years
1TB= 35 millenia
1PB = 36 M years
1 byte = 1 second
1KB = 17 mins
1MB = 12 days
1GB = 34 years
1TB= 35 millenia
1PB = 36 M years
1EB = 10 × age of universe
(Last year, probably about 15 ZB of data was produced)
A current desktop computer has a clockspeed of 3GHz
A current desktop computer has a clockspeed of 3GHz.
In other words: a computer's clock ticks as many times PER SECOND as a regular clock does during a person's life (a long life).
So how can we understand what 3GHz really means?
Let's slow the computer right down slow.
Slowmo guys have a video where when you slow it down, you see something completely different. Let's slow a computer down to 1Hz, and see what is going on.
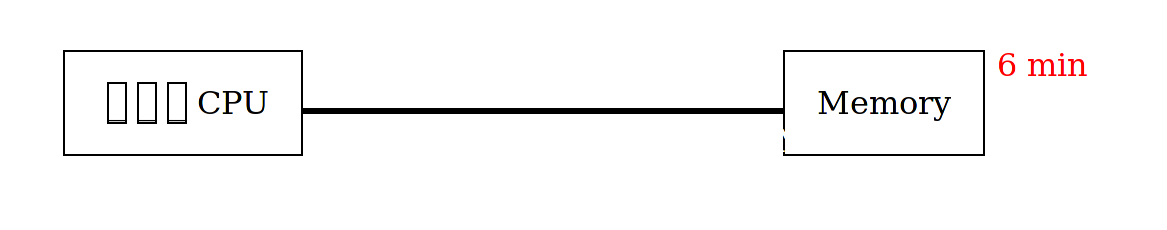
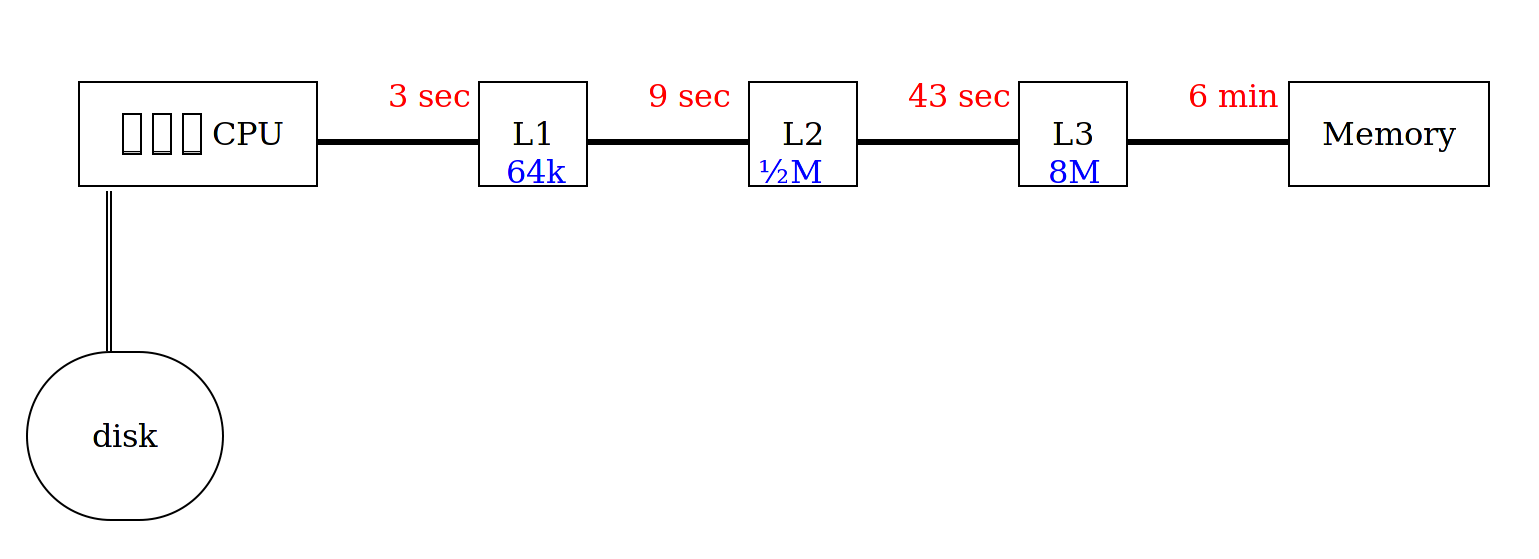
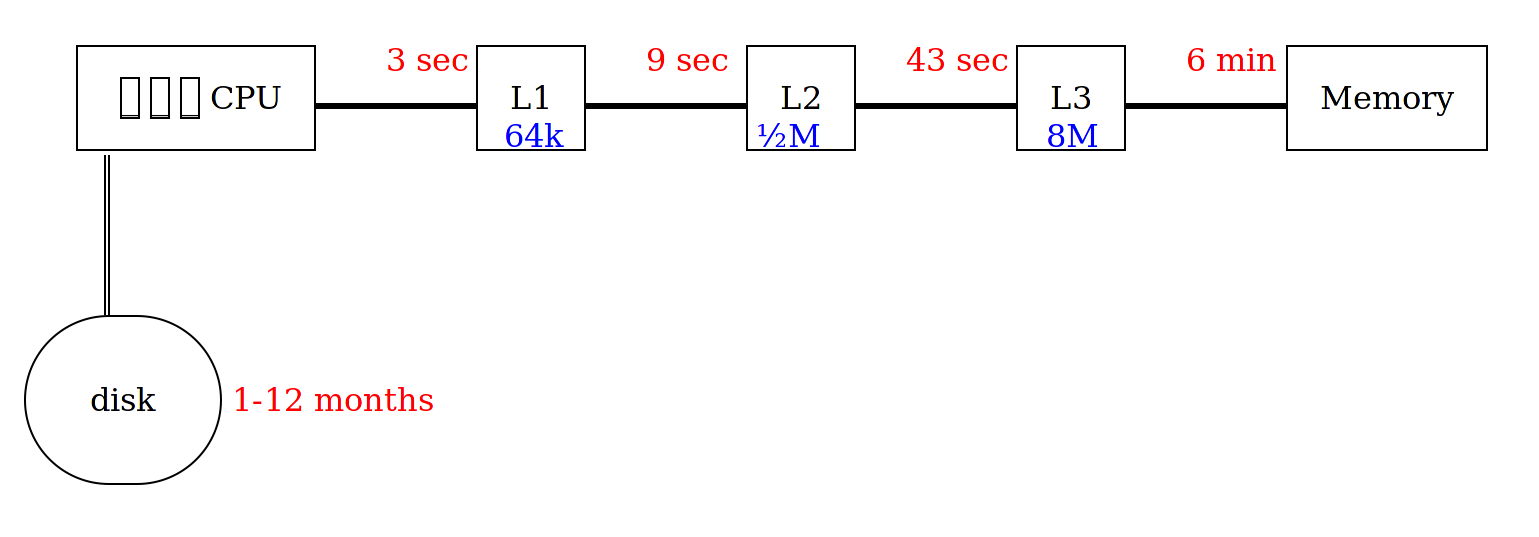
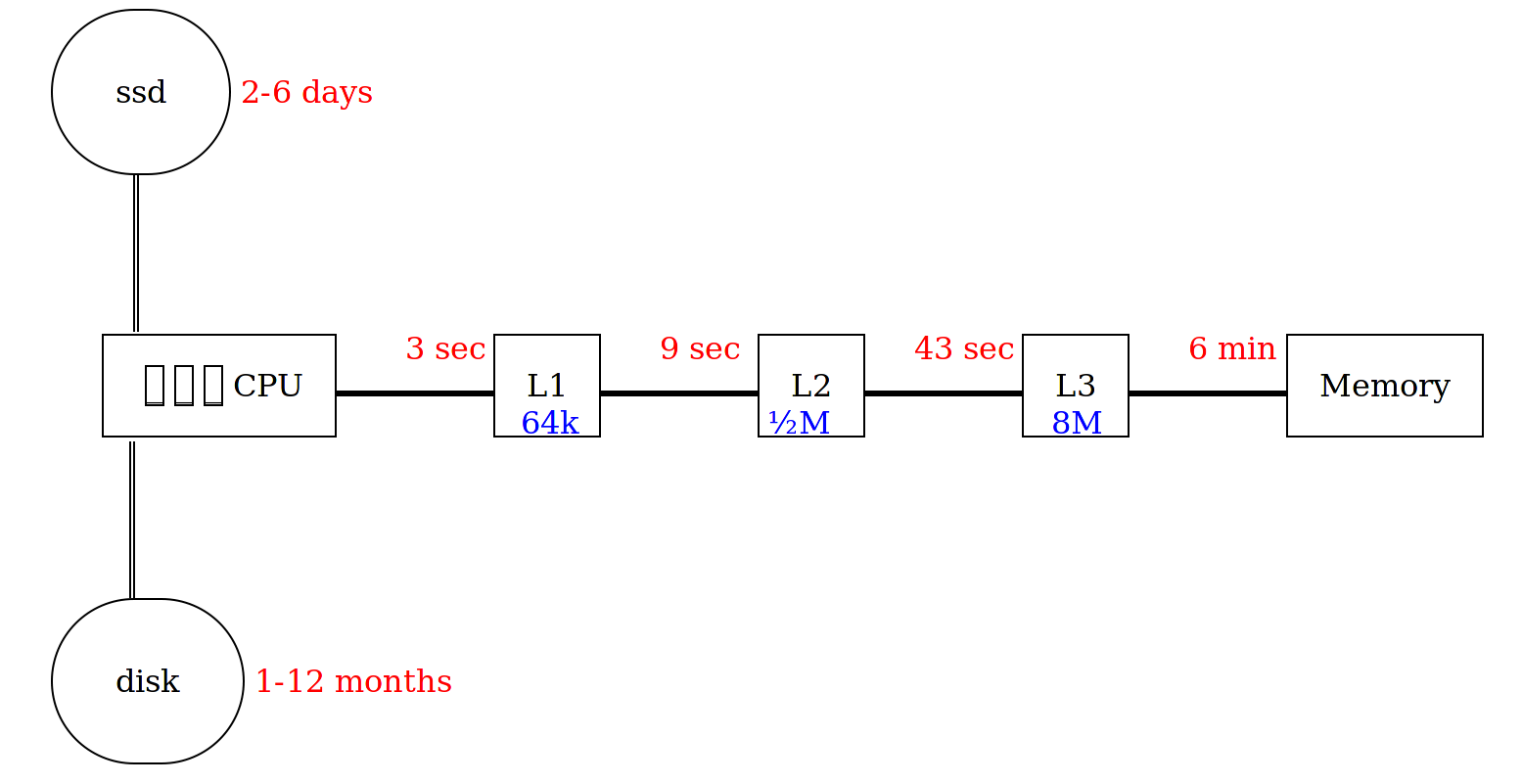
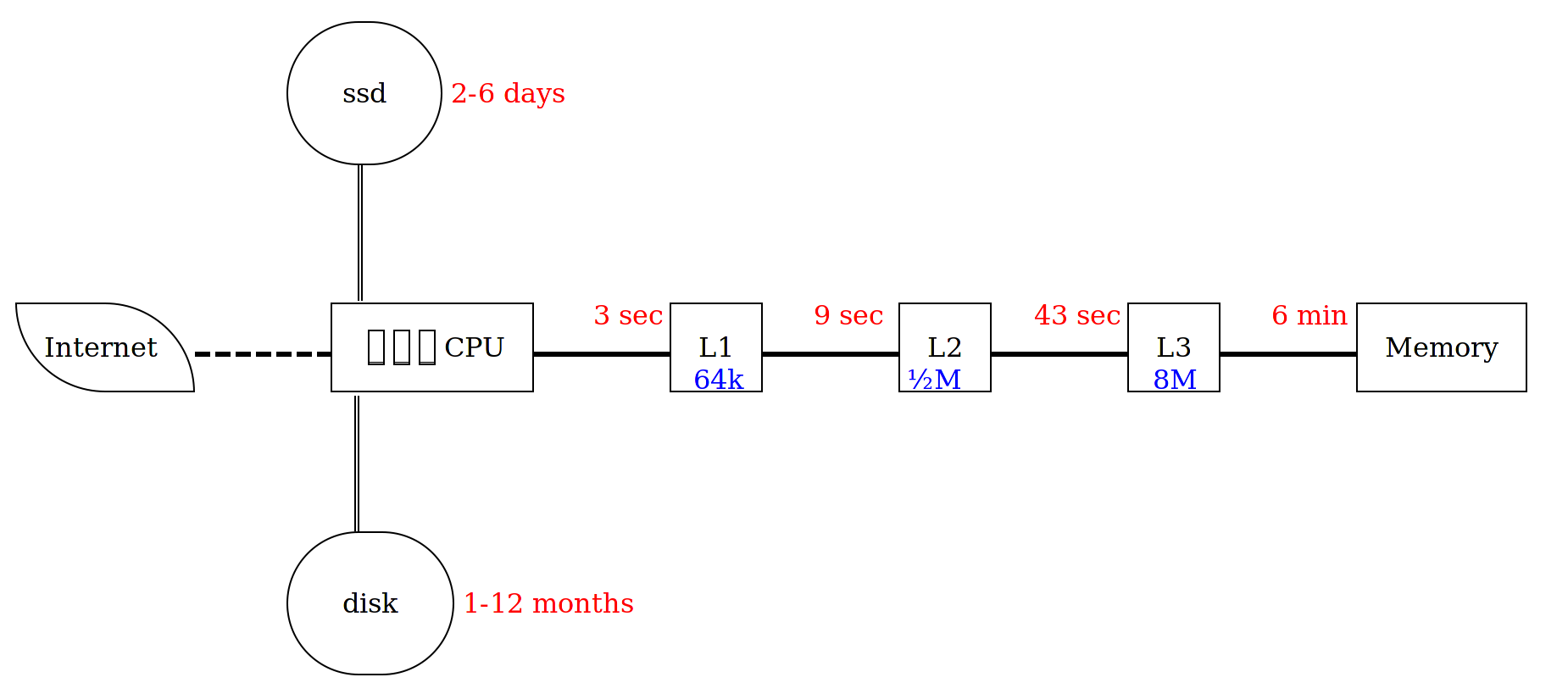
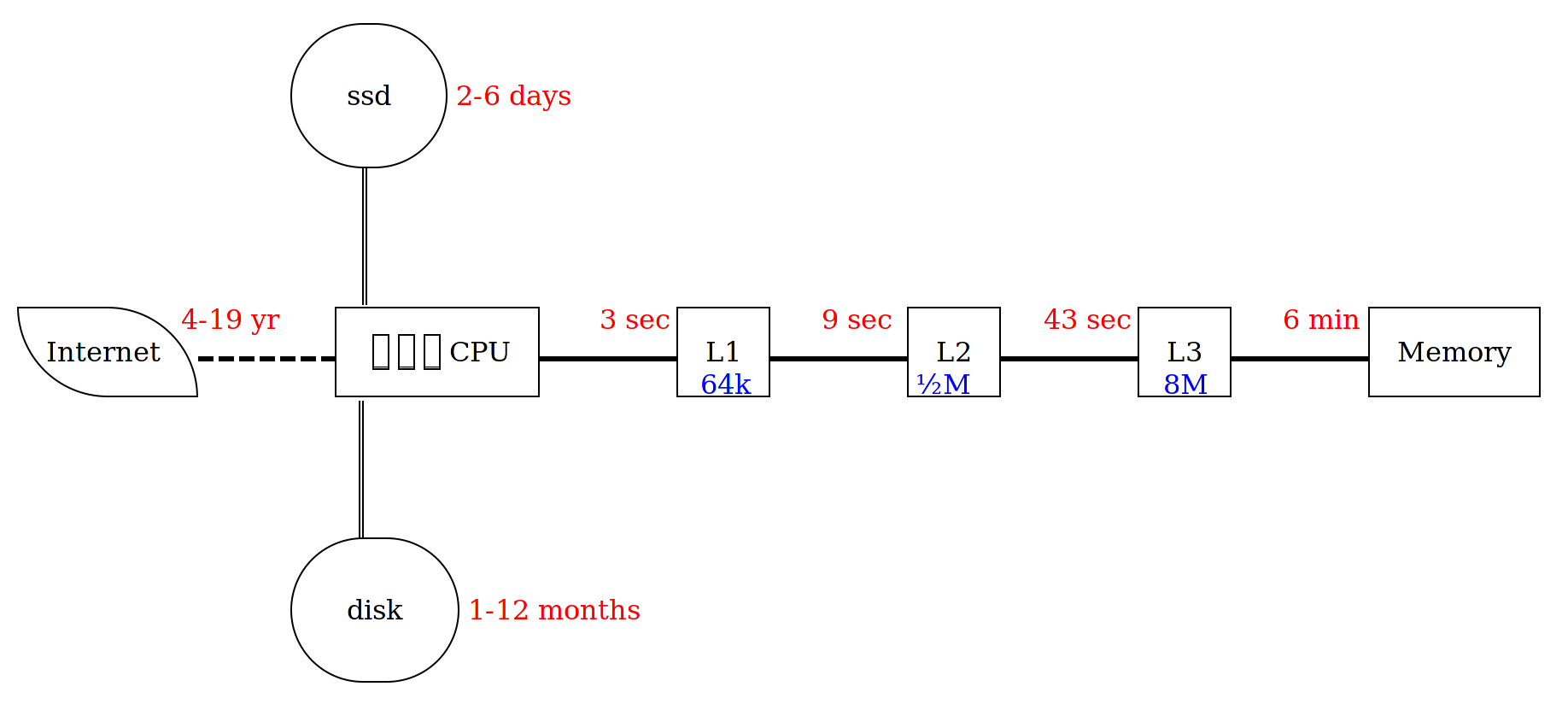
Each cache is smaller, quicker, and much more expensive than the next.
Note that each cache is about 10× larger than the previous.
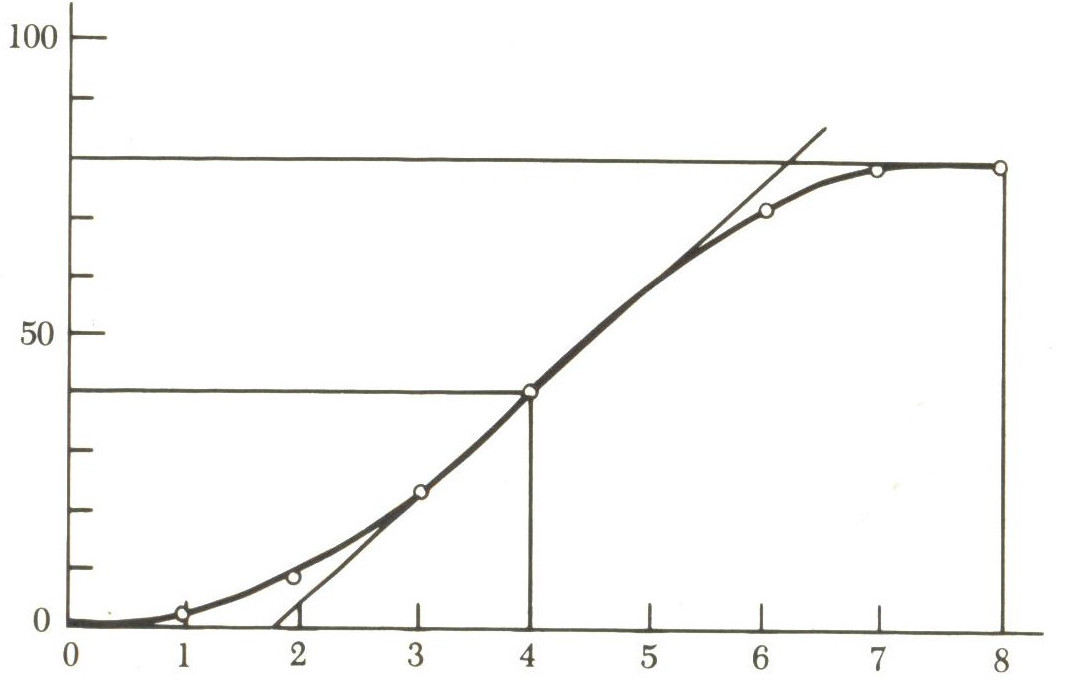According to La Solla-Price, most real-life exponentials with a natural limit
actually follow a logistic curve.
And he says, there are a number of ways that a logistical curve reaches its limit.
Loss of definition
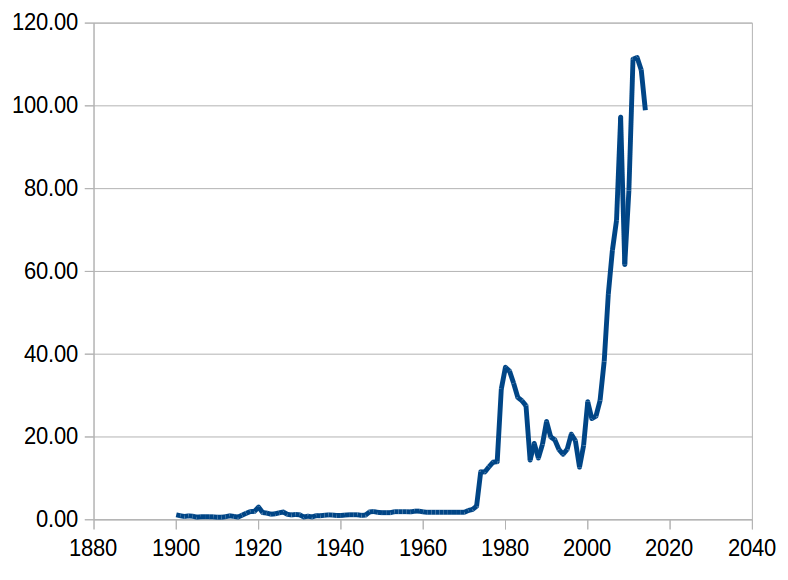
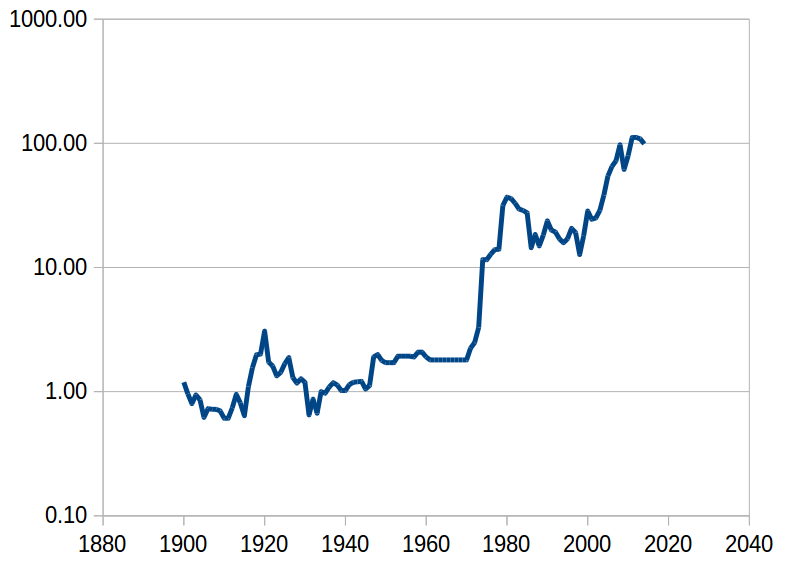
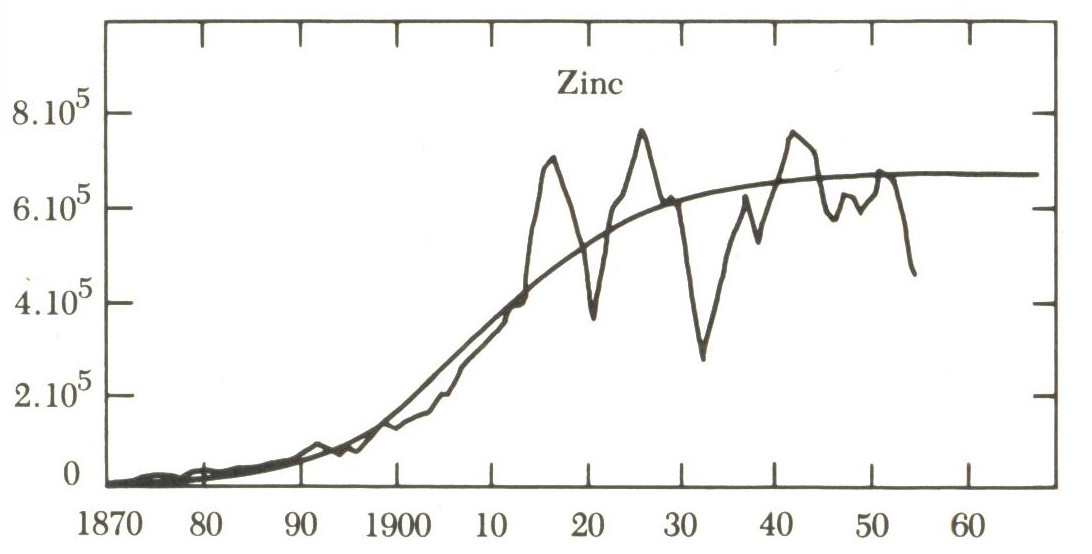
A possible contender for "Loss of definition"
Convergent Oscillation
A possible contender for convergent oscillation
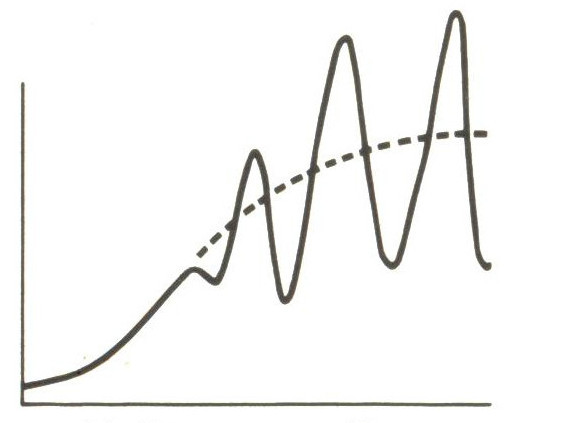
Divergent Oscillation
Possible divergent oscillation
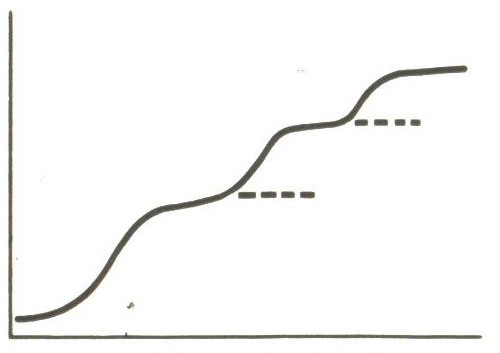
Escalation
Escalation
We know that there are physical limits to Moore's Law.
The question is, which sort of death will Moore's Law die?
Ray Kurzweil discovered that Moore's Law is just one part of a progression
going back at least as far as 1900
He calculated how many multiplications you could get for $1000 using 4 generations of technologies, Electromechanical, Relays, Valves and Transistors, and shows that the progression that we call Moore's Law has been going since at least 1900. Here is computing in 1920.
This suggests that Moore's Law is just part of a series of escalations, as each new technology comes along.
Several new possibilities are already on the horizon, such as light computing and quantum computing. What seems likely is that by the time Moore's Law peters out, a new technology will be there to replace it.
Moore's Law is still alive and well
Even though it has natural limits, past data suggests it is part of a higher law that will continue even after integrated circuits have reached their maximum density.
.svg#/media/File:DJIA_historical_graph_to_jul11_(log).svg){kind=link}
